Ein Crash-Kurs im kaufmännischen Rechnen

Vielseitig anwendbar: Der Dreisatz

Aufgaben im (Geschäfts-) Leben
Generationen von Schülern haben beim intensiven Einüben des Dreisatzes gestöhnt – und ihn erstaunlicherweise gleich anschließend wieder vergessen. Dabei begegnen einem im (Geschäfts-)Leben täglich unzählige Aufgaben, die sich per Dreisatz einfach und schnell lösen lassen.

Beispiel
Aufgabe 1: Material kalkulieren
Norbert Bell kalkuliert ein Angebot für die Folienbeschriftung von Fahrzeugen. Beim letzten Auftrag hat er für 3 VW-Busse insgesamt 28,80 m Folie verbraucht. Nun bestellt der Kunde Beschriftungen für 2 weitere VW-Busse. Wie viel Folie wird dafür benötigt?

Aus 3 Größen eine 4. ableiten
Wenn du deine Mitarbeiter diese Aufgabe betrachten lässt, sollte ihnen klar werden, warum der „Dreisatz“ so heißt: Es sind 3 Größen bekannt, aus denen eine 4. errechnet wird. Voraussetzung für die Anwendbarkeit des Dreisatzes ist zudem, dass es einen logischen Zusammenhang zwischen der Entwicklung dieser Größen gibt.

Lösung der Aufgabe 1 mit dem geraden Dreisatz:
Im Beispielfall lautet die logische Beziehung: Je mehr Fahrzeuge zu beschriften sind, desto mehr Folie wird gebraucht (mathematisch ausgedrückt: „direkt proportionale“ Beziehung). Sie rechnen mit einem sogenannten geraden Dreisatz – das geht so:

Schritt 1: Du schreibst die logischen Beziehungen („wenn – dann“) untereinander auf:

• wenn 3 VW-Busse, dann 28,80 m Folie
• wenn 2 VW-Busse, dann ??? m Folie

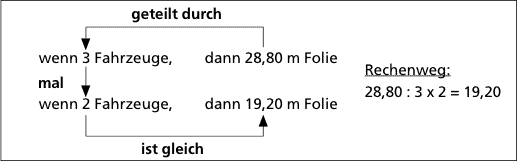
Schritt 2: Du ermittelst den Wert für eine Einheit, also den Folienbedarf für 1 VW-Bus:
28,80 m : 3 VW-Busse = 9,60 m/VW-Bus

Schritt 3: Du multiplizierst die einzelne Einheit (hier den Folienbedarf pro VW-Bus) mit der gefragten Menge:
9,60 m x 2 Busse = 19,20 m

Gerader Dreisatz („Je mehr, desto mehr“):

Es gibt auch indirekt proportionale Beziehungen, die nach dem Prinzip „Je mehr, desto weniger“ (oder „Je weniger, desto mehr“) funktionieren. In diesen Fällen wenden Sie den ungeraden Dreisatz an.

Beispiel
Aufgabe 2: Arbeitsstunden berechnen

Roswitha Koch verhandelt mit einer Kundin über die Fensterreinigung in ihrem modernen Haus, das sehr viele Glasflächen hat. Die Kundin bittet: „Das letzte Mal waren 2 Leute ab 9 Uhr 7,5 Stunden beschäftigt. Schicken Sie mir dieses Mal bitte einen 3. Mann mit, weil die Arbeit um 14 Uhr fertig sein muss.“ Roswitha Koch rechnet aus, ob das funktionieren wird: Wenn 2 Mitarbeiter 7,5 Stunden benötigt haben, wie schnell sind dann 3 Personen?

Lösung der Aufgabe 2 mit dem ungeraden Dreisatz:
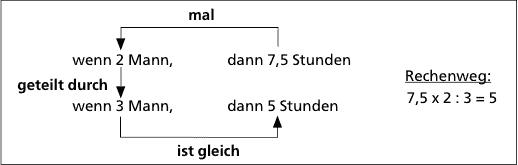
Die Beziehung zwischen den Größen ist indirekt proportional: je mehr Leute, desto weniger Stunden. Gerechnet wird mit dem ungeraden Dreisatz, bei dem erst multipliziert und dann geteilt wird: 7,5 Stunden x 2 Mitarbeiter : 3 Mitarbeiter = 5 Stunden. Wenn 3 Mann um 9 Uhr anfangen, müssten sie also um 14 Uhr fertig sein.

Ungerader Dreisatz („Je mehr, desto weniger“):

Alles auf Hundert bezogen: Die Prozentrechnung

 Grundwert = 100 setzen
Die Prozentrechnung gehört zum Muss-Wissen für jeden, der am Wirtschaftsleben teilnimmt. Sie erlaubt es, Größen zueinander ins Verhältnis zu setzen, indem eine Größe – etwa ein nicht reduzierter Preis – als Grundwert gleich 100 gesetzt wird. Fragen nach dem Schema „Wie viel sind 12 % von 250 €?“ sind dadurch mit dem Dreisatz zu lösen.

Prozentrechnung:

Prozentwert   = Grundwert  x Prozentsatz / 100

30€                 = 250€           x 12                / 100

Beispiel
Aufgabe 3: Rabatt berechnen
Weinhändler Karl Fischer verhandelt beim Einkauf mit einem Winzer: „Die Kiste zu 12 Flaschen kostet 43,20 € netto. Wenn Sie 6 Kisten nehmen, gebe ich Ihnen auf alle 2,5 % Rabatt.“ Karl Fischer rechnet nach, ob sich das für ihn lohnt: Der Grundwert ist der Kistenpreis von 43,20 €. Den teilt Karl Fischer durch 100 und multipliziert das Hundertstel mit dem Rabatt-Prozentsatz, also mit 2,5. Die Rechnung: 43,20 € : 100 x 2,5 = 1,08 € Rabatt pro Kiste.

Verminderter Grundwert
Oft willst du ausrechnen, was eine Sache nach Abzug eines Rabattbetrags kostet. Dafür gibt es 2 Rechenwege:

• Entweder man berechnet erst den Prozentwert und zieht diesen dann vom Grundwert ab,
• oder man berechnet gleich den verminderten Grundwert. Dieser Weg ist der schnellere, wie das folgende Beispiel zeigt.

Beispiel
Aufgabe 4: Preis nach Rabattabzug ermitteln
Boutiquenbesitzerin Marlies Winter weist ihre Aushilfe Aishe an: „Diese Tops zeichnen wir um 20 % herunter.“

Aishe überlegt: Die Tops kosten 29,95 €. 20 % davon sind laut geradem Dreisatz 29,95 € : 100 x 20 = 5,99 €. Die zieht sie vom bisherigen Preis ab:
Die Tops sollen also 29,95 ./. 5,99 = 23,96 € kosten.

Bei erneuter Betrachtung fällt Aishe auf, wie sie noch schneller hätte rechnen können: „Wenn ich 20 % abziehen soll, heißt das, dass der neue Preis 80 % des alten Preises ausmacht. Dann rechne ich einfach so: 29,95 € (alter Preis) : 100 x 80 = 23,96 € (neu- er Preis).

Formel zur Berechnung des verminderten Grundwerts:

Rabattierter Preis = (Ausgangspreis x (100 ./. Rabatt-Prozentsatz)) / 100

Brutto, netto und zurück: Die Umsatzsteuer

Wenn du (oder ein Mitarbeiter) Preise kalkulieren bzw. Rechnungen schreiben, schlägst du die Umsatzsteuer (19 oder 7 %) auf den Rechnungsbetrag auf. So wird aus deinem Netto-Rechnungsbetrag der Brutto- Betrag, den dein Kunde zu zahlen hat. Du ahnst es schon: Auch bei Umsatzsteuer-Berechnungen spielt der Dreisatz eine entscheidende Rolle. Wenn du Umsatzsteuer aufschlägst, machst du das, indem du den vermehrten Grundwert ermittelst.

Formel zur Berechnung des vermehrten Grundwerts:

Brutto-Betrag = (Netto-Betrag x (100 + USt.-Satz)) / 100

Beispiel:
Aufgabe 5: Brutto-Preis ermitteln

Der Grafiker Jens Müller stellt eine Rechnung über ein Logo, das er für ein Hotel entwickelt hat. Vereinbart war ein Pauschalpreis von 450 € zzgl. 19 % USt. Der Netto-Preis ist der Grundwert, und den Brutto-Preis – also den vermehrten Grundwert –errechnet Müller so: 450 € netto x (100 + 19) : 100 = 535,50 € brutto

Umgekehrt sollten deine Mitarbeiter auch aus Brutto- Preisen die Netto-Beträge ermitteln können. Ein häufiger Fehler ist es dabei, vom Brutto-Betrag einfach 19 oder 7 % abzuziehen! Richtig funktioniert es wieder mit dem Dreisatz.

Netto-Betrag errechnen:

Netto-Betrag = (Brutto-Betrag x 100) / (100 +USt.-Satz)

Beispiel
Aufgabe 6: Netto-Rechnungsbetrag ermitteln

Händlerin Astrid Zügli verkauft einen Teppich für 595 €. Ein Geschäftskunde will den Netto-Preis wissen. Den berechnet Astrid Zügli per Dreisatz so: 595 € : 119 x100 = 500 € netto

PRAXIS-TIPP

Bei der Umsatzsteuer die Formeln kürzen!

Da die Prozentsätze 19 und 7 % fix sind, tauchen bei Umsatzsteuer-Aufschlägen immer dieselben Brüche auf, nämlich 119 : 100 (= 1,19) bzw. 107 : 100 (= 1,07). Schnelle Rechner ersparen sich daher den Umweg über den Dreisatz und rechnen so:

19 % USt.
Netto-Betrag x 1,19 = Brutto-Betrag
Brutto-Betrag : 1,19 = Netto-Betrag

7 % USt.
Netto-Betrag x 1,07 = Brutto-Betrag
Brutto-Betrag : 1,07 = Netto-Betrag

Aus wenig mach mehr: Die Zinsrechnung

Prozentrechnung inklusive des Faktors Zeit
Die Zinsrechnung ist im Grunde auch „nur“ eine Prozentrechnung, bei der allerdings die Zeit eine wesentliche Rolle spielt. Entsprechend werden die Elemente Grundwert (= Kapital), Prozentsatz (= Zinssatz) und Prozentwert (= Zinsbetrag) um die Zeitspanne ergänzt, über die hinweg der Geldbetrag ent- bzw. verliehen wird.

Geld anlegen – Guthabenzins kassieren
Wer Geld anlegt, bekommt dafür oft Guthabenzinsen. Der Zinssatz, den dir das Kreditinstitut bietet, wird immer als Jahreszinssatz angegeben, der durch das Kürzel „p.a.“ gekennzeichnet ist (von lat. pro anno = pro Jahr). Möchtest du nur den Zinsbetrag berechnen, geht das einfach mit dem Dreisatz.

Jahreszinsbetrag = (Kapital x Zinssatz p.a.) / 100

Beispiel:
Aufgabe 7: Zinsbetrag berechnen

Handwerker Ranulf Groß hat aus dem Verkauf nicht mehr genutzter Maschinen 2.500 € erlöst. Diese benötigt er nicht als Liquiditätsreserve und möchte sie deswegen für 1 Jahr anlegen. Dafür bietet ihm seine Bank einen Zinssatz von 1,8 % p.a. Somit er- hält er nach einem Jahr

2.500 € : 100 x 1,8 = 2.500 x 0,018 = 45 € Zinsen.

Willst du die Höhe des neuen Kapitals nach Gutschrift der Zinsen berechnen, verwendest du die Formel für den vermehrten Grundwert.

Kapital nach Jahresverzinsung = Anfangskapital X (100 + Zinssatz p.a.) / 100

Beispiel
Aufgabe 8: Kapital nach Verzinsung berechnen

Handwerker Ranulf Groß aus dem obigen Beispiel fragt sich, wie viel Geld er nach einem Jahr zu- rückerhält. Er rechnet so: 2.500 € Anfangskapital x 101,8 : 100 = 2.545 € neues Kapital. Als ökonomischer Rechner kürzt er das so: 2.500 € x 1,018 = 2.545 €.

Zinseszinseffekt

Wer sein Geld längerfristiger anlegt, kann doppelt profitieren: Zum einen gibt es für längerfristige Anlagen höhere Zinssätze, zum anderen kommt dann der Zinseszinseffekt zum Tragen: Wenn der in einem Jahr erwirtschaftete Zins nicht ausgeschüttet wird, sondern das zu verzinsende Kapital erhöht, steigt auch der Zinsbetrag. Der Zinseszinseffekt wirkt umso stärker, je höher der Zinssatz und je länger der Anlagezeitraum ist. Allerdings ist seine manuelle Berechnung umständlich. Ökonomische Rechner verwenden deswegen die

Zinseszinsformel:
Endkapital = Anfangskapital x (Zinssatz p.a. / 100 + 1^Jahre)

Beispiel:
Aufgabe 9: Zinseszins berechnen
Ranulf Groß legt 2.500 € für 5 Jahre an. Dafür bekommt er einen Zinssatz von 2,9 %. Nach den 5 Jahren ist sein Kapital so gewachsen: 2.500 x (1,029)5 = 2.884,14 €

Kredite aufnehmen – Schuldzinsen zahlen
Die meisten Selbstständigen und Unternehmer können erforderliche Investitionen nicht komplett aus eigenen Mitteln finanzieren, sondern müssen dafür Kredite bei Kreditinstituten oder privaten Gläubigern aufnehmen. Natürlich zahlen sie dann Zinsen dafür. Den Zins- bzw. Rückzahlungsbetrag, der nach einem oder mehreren Jahren fällig ist, berechnest du wie bei Guthabenzinsen.

Jahreszins herunterrechnen
Im kaufmännischen Leben werden Kredite aber nicht nur über Jahre, sondern auch für Monate oder nur Tage vergeben. Dann musst du den Jahreszinssatz (p.a.) auf die kürzere Laufzeit umrechnen. Beachte dabei: Für Kaufleute hat das Jahr nur 360 und jeder Monat 30 Tage.

Zeitgenaue Zinsberechnung:
Monatszins    = Kapital x Zinssatz p.a. / 100 x Monate/12
Tageszins       = Kapital x Zinssatz p.a. / 100 x Tage/360

Beispiel
Aufgabe 10: Monats- und Tageszins berechnen

Malermeisterin Brigitte König benötigt einen Kredit, um einen Liquiditätsengpass zu überbrücken. Sie nimmt 3.000 € für 5 Monate auf. Dafür verlangt die Bank einen Zinssatz von 4,95 % p.a. Der Monats- zins beträgt:

3.000 € x 4,95 : 100 x 5 : 12 = 61,88 €

Zudem hat die Bank Brigitte König einen Kontokorrentkredit zum Zinssatz 10,25 % p.a. eingeräumt. Nimmt sie 3.000 € für 150 Tage in Anspruch, kostet das

3.000 € x 10,25 : 100 x 150 : 360 = 128,13 €

Oft unterschätzt: Lieferantenkredit mit Skonto
Skontoklausel verstehen
Unter Kaufleuten ist es üblich, Kunden Zahlungsziele einzuräumen. Häufig bietet der Aussteller der Rechnung einen Abzug (= Skonto), wenn sein Kunde sofort bar bezahlt oder den Betrag binnen einer kurzen Frist überweist. Dann findet sich auf der Rechnung beispielsweise eine solche Klausel: „3 % Skonto bei Zahlung binnen 10 Tagen, sonst 30 Tage netto Kasse.“

Kluge (und liquide) Unternehmer zahlen schnell und ziehen den Skontobetrag von der Rechnung ab. Denn sie wissen: Wer die längere Zahlungsfrist nutzt, nimmt einen Lieferantenkredit in Anspruch, der sehr, sehr teuer ist. Wie teuer? Das lässt sich schnell mithilfe einer Näherungsformel abschätzen.

Zinsen für einen Lieferantenkredit:

Jahreszins = Skontosatz x 360 / (Zahlungsziel ./. Skontofrist)

Beispiel
Aufgabe 11: Jahreszinssatz des Lieferantenkredits berechnen

Bei „3% Skonto binnen 10 Tagen oder 30 Tage netto Kasse“ beträgt der Jahreszinssatz nach der Näherungsformel: 3 x 360 : (30 ./. 10) = 54 %

Umgerechnet auf ein Jahr würde der Lieferantenkredit also 54 % an Zinsen kosten – so etwas nutzt kein vernünftiger Selbstständiger oder Unternehmer, wenn er liquide Mittel hat oder einen günstigeren Kredit – etwa den Kontokorrentkredit – für das Zahlen innerhalb der Skontofrist ausschöpfen kann!

Für deine Pinnwand: Die kaufmännischen Formeln im Überblick

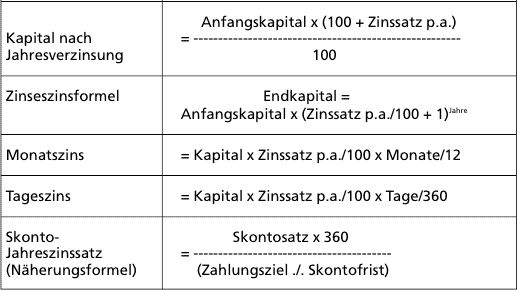
Vorlage: www.selbststaendig.com -> Vorlagen – > kaufmännische Formeln

Dieser Artikel wurde von BWRmed!a bereitgestellt.
Autor: Günter Stein (Unternehmer)